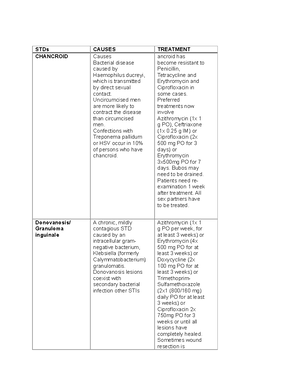
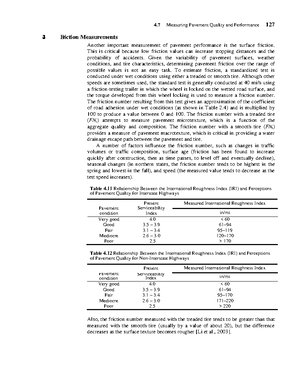
- Information
- AI Chat
Special Random Variables
BS Civil Engineering
University of Nueva Caceres
Recommended for you
Preview text
Chapter 5
SPECIAL RANDOM VARIABLES
Certain types of random variables occur over and over again in applications. In this chapter, we will study a variety of them.
5 THE BERNOULLI AND BINOMIAL
RANDOM VARIABLES
Suppose that a trial, or an experiment, whose outcome can be classified as either a “success” or as a “failure” is performed. If we let X = 1 when the outcome is a success and X = 0 when it is a failure, then the probability mass function of X is given by
P{X = 0 } = 1 − p (5.1) P{X = 1 } = p
where p, 0 ≤ p ≤ 1, is the probability that the trial is a “success.” A random variable X is said to be a Bernoulli random variable (after the Swiss mathe- matician James Bernoulli) if its probability mass function is given by Equations 5.1 for some p ∈ (0, 1). Its expected value is
E [X ] = 1 · P{X = 1 } + 0 · P{X = 0 } = p
That is, the expectation of a Bernoulli random variable is the probability that the random variable equals 1. Suppose now that n independent trials, each of which results in a “success” with prob- ability p and in a “failure” with probability 1 − p, are to be performed. If X represents the number of successes that occur in the n trials, then X is said to be a binomial random variable with parameters (n, p).
141
142 Chapter 5: Special Random Variables
The probability mass function of a binomial random variable with parameters n and p is given by
P{X = i} =
(
n i
)
pi ( 1 − p)n−i , i = 0, 1,... , n (5.1)
where
( n i
)
= n!/[i!(n − i)!] is the number of different groups of i objects that can be chosen from a set of n objects. The validity of Equation 5.1 may be verified by first noting that the probability of any particular sequence of the n outcomes containing i successes and n − i failures is, by the assumed independence of trials, pi ( 1 − p)n−i . Equation 5.1 then follows since there are
( n i
)
different sequences of the n outcomes leading to i successes and n − i failures — which can perhaps most easily be seen by noting that there are
( n i
)
different selections of the i trials that result in successes. For instance, if n = 5, i = 2, then there are
( 5
2
)
choices of the two trials that are to result in successes — namely, any of the outcomes
(s, s, f , f , f ) ( f , s, s, f , f ) ( f , f , s, f , s) (s, f , s, f , f ) ( f , s, f , s, f ) (s, f , f , s, f ) ( f , s, f , f , s) ( f , f , f , s, s) (s, f , f , f , s) ( f , f , s, s, f )
where the outcome ( f , s, f , s, f ) means, for instance, that the two successes appeared on trials 2 and 4. Since each of the
( 5
2
)
outcomes has probability p 2 ( 1 − p) 3 , we see that the probability of a total of 2 successes in 5 independent trials is
( 5
2
)
p 2 ( 1 − p) 3. Note that, by the binomial theorem, the probabilities sum to 1, that is,
∑ ∞
i= 0
p(i) =
∑ n
i= 0
( n i
)
pi ( 1 − p)n−i = [p + ( 1 − p)]n = 1
The probability mass function of three binomial random variables with respective parame- ters (10, .5), (10, .3), and (10, .6) are presented in Figure 5. The first of these is symmetric about the value .5, whereas the second is somewhat weighted, or skewed, to lower values and the third to higher values. EXAMPLE 5 It is known that disks produced by a certain company will be defective with probability .01 independently of each other. The company sells the disks in packages of 10 and offers a money-back guarantee that at most 1 of the 10 disks is defective. What proportion of packages is returned? If someone buys three packages, what is the probability that exactly one of them will be returned? SOLUTION If X is the number of defective disks in a package, then assuming that customers always take advantage of the guarantee, it follows that X is a binomial random variable
144 Chapter 5: Special Random Variables
Because each package will, independently, have to be replaced with probability .005, it follows from the law of large numbers that in the long run .5 percent of the packages will have to be replaced. It follows from the foregoing that the number of packages that the person will have to return is a binomial random variable with parameters n = 3 and p = .005. Therefore, the
probability that exactly one of the three packages will be returned is
(
3 1
)
(.005)(.995) 2 =
.015. ■
EXAMPLE 5 The color of one’s eyes is determined by a single pair of genes, with the gene for brown eyes being dominant over the one for blue eyes. This means that an individual having two blue-eyed genes will have blue eyes, while one having either two brown-eyed genes or one brown-eyed and one blue-eyed gene will have brown eyes. When two people mate, the resulting offspring receives one randomly chosen gene from each of its parents’ gene pair. If the eldest child of a pair of brown-eyed parents has blue eyes, what is the probability that exactly two of the four other children (none of whom is a twin) of this couple also have blue eyes?
SOLUTION To begin, note that since the eldest child has blue eyes, it follows that both parents must have one blue-eyed and one brown-eyed gene. (For if either had two brown- eyed genes, then each child would receive at least one brown-eyed gene and would thus have brown eyes.) The probability that an offspring of this couple will have blue eyes is equal to the probability that it receives the blue-eyed gene from both parents, which is
( 1
2
)( 1
2
)
= 14.
Hence, because each of the other four children will have blue eyes with probability 14 , it follows that the probability that exactly two of them have this eye color is
( 4 2
)
(1/4) 2 (3/4) 2 = 27/128 ■
EXAMPLE 5 A communications system consists of n components, each of which will, independently, function with probability p. The total system will be able to operate effec- tively if at least one-half of its components function.
(a) For what values of p is a 5-component system more likely to operate effectively than a 3-component system? (b) In general, when is a 2k + 1 component system better than a 2k − 1 component system?
SOLUTION (a) Because the number of functioning components is a binomial random variable with parameters (n, p), it follows that the probability that a 5-component system will be effective is ( 5 3
)
p 3 ( 1 − p) 2 +
(
5
4
)
p 4 ( 1 − p) + p 5
5 The Bernoulli and Binomial Random Variables 145
whereas the corresponding probability for a 3-component system is ( 3 2
)
p 2 ( 1 − p) + p 3
Hence, the 5-component system is better if
10 p 3 ( 1 − p) 2 + 5 p 4 ( 1 − p) + p 5 ≥ 3 p 2 ( 1 − p) + p 3
which reduces to
3 ( p − 1 ) 2 ( 2 p − 1 ) ≥ 0
or
p ≥
1
2
(b) In general, a system with 2k + 1 components will be better than one with 2k − 1 components if (and only if ) p ≥ 12. To prove this, consider a system of 2k + 1 components and let X denote the number of the first 2k − 1 that function. Then
P 2 k+ 1 (effective) = P{X ≥ k + 1 } + P{X = k}( 1 − ( 1 − p) 2 ) + P{X = k − 1 } p 2
which follows since the 2k + 1 component system will be effective if either (1) X ≥ k + 1; (2) X = k and at least one of the remaining 2 components function; or (3) X = k − 1 and both of the next 2 function. Because
P 2 k− 1 (effective) = P{X ≥ k} = P{X = k} + P{X ≥ k + 1 }
we obtain that
P 2 k+ 1 (effective) − P 2 k− 1 (effective)
= P{X = k − 1 } p 2 − ( 1 − p) 2 P{X = k}
=
(
2 k − 1 k − 1
)
pk− 1 ( 1 − p)k p 2 − ( 1 − p) 2
(
2 k − 1 k
)
pk ( 1 − p)k− 1
=
(
2 k − 1 k
)
pk ( 1 − p)k [p − ( 1 − p)] since
(
2 k − 1 k − 1
)
=
(
2 k − 1 k
)
≥ 0 ⇔ p ≥
1
2
■
5 The Bernoulli and Binomial Random Variables 147
Var(X ) =
∑ n
i= 1
Var(Xi ) since the Xi are independent
= np( 1 − p)
If X 1 and X 2 are independent binomial random variables having respective parameters (ni , p), i = 1, 2, then their sum is binomial with parameters (n 1 + n 2 , p). This can most easily be seen by noting that because Xi , i = 1, 2, represents the number of successes in ni independent trials each of which is a success with probability p, then X 1 + X 2 represents the number of successes in n 1 + n 2 independent trials each of which is a success with probability p. Therefore, X 1 + X 2 is binomial with parameters (n 1 + n 2 , p).
5.1 Computing the Binomial Distribution Function
Suppose that X is binomial with parameters (n, p). The key to computing its distribution function
P{X ≤ i} =
∑ i
k= 0
(
n k
)
pk ( 1 − p)n−k , i = 0, 1,... , n
is to utilize the following relationship between P{X = k + 1 } and P{X = k}:
P{X = k + 1 } =
p 1 − p
n − k k + 1
P{X = k} (5.1)
The proof of this equation is left as an exercise.
EXAMPLE 5 Let X be a binomial random variable with parameters n = 6, p = .4. Then, starting with P{X = 0 } = (.6) 6 and recursively employing Equation 5.1, we obtain
P{X = 0 } = (.6) 6 =.
P{X = 1 } = 4661 P{X = 0 } =.
P{X = 2 } = 4652 P{X = 1 } =.
P{X = 3 } = 4643 P{X = 2 } =.
P{X = 4 } = 4634 P{X = 3 } =. P{X = 5 } = 4625 P{X = 4 } =.
P{X = 6 } = 4616 P{X = 5 } = .0041 ■
The text disk uses Equation 5.1 to compute binomial probabilities. In using it, one enters the binomial parameters n and p and a value i and the program computes the probabilities that a binomial (n, p) random variable is equal to and is less than or equal to i.
148 Chapter 5: Special Random Variables
Binomial Distribution
Enter Value For p:
Enter Value For n:
Enter Value For i:
.
100
70
Probability (Number of Successes 5 i ). Probability (Number of Successes < 5 i ).
Start
Quit
FIGURE 5.
EXAMPLE 5 If X is a binomial random variable with parameters n = 100 and p = .75, find P{X = 70 } and P{X ≤ 70 }. SOLUTION The text disk gives the answers shown in Figure 5. ■
5 THE POISSON RANDOM VARIABLE
A random variable X, taking on one of the values 0, 1, 2,... , is said to be a Poisson random variable with parameter λ, λ > 0, if its probability mass function is given by
P{X = i} = e−λ
λi i!
, i = 0, 1,... (5.2)
The symbol e stands for a constant approximately equal to 2. It is a famous constant in mathematics, named after the Swiss mathematician L. Euler, and it is also the base of the so-called natural logarithm. Equation 5.2 defines a probability mass function, since
∑ ∞
i= 0
p(i) = e−λ
∑ ∞
i= 0
λi /i! = e−λeλ = 1
A graph of this mass function when λ = 4 is given in Figure 5. The Poisson probability distribution was introduced by S. D. Poisson in a book he wrote dealing with the application of probability theory to lawsuits, criminal trials, and the like. This book, published in 1837, was entitled Recherches sur la probabilité des jugements en matière criminelle et en matière civile.
150 Chapter 5: Special Random Variables
Evaluating at t = 0 gives that
E [X ] = φ′( 0 ) = λ Var(X ) = φ′′( 0 ) − (E [X ]) 2 = λ 2 + λ − λ 2 = λ
Thus both the mean and the variance of a Poisson random variable are equal to the parameter λ. The Poisson random variable has a wide range of applications in a variety of areas because it may be used as an approximation for a binomial random variable with parameters (n, p) when n is large and p is small. To see this, suppose that X is a binomial random variable with parameters (n, p) and let λ = np. Then
P{X = i} =
n! (n − 1 )!i!
pi ( 1 − p)n−i
=
n! (n − 1 )!i!
(
λ n
)i ( 1 −
λ n
)n−i
=
n(n − 1 )... (n − i + 1 ) ni
λi i!
( 1 − λ/n)n ( 1 − λ/n)i
Now, for n large and p small,
( 1 −
λ n
)n ≈ e−λ
n(n − 1 )... (n − i + 1 ) ni
≈ 1
(
1 −
λ n
)i ≈ 1
Hence, for n large and p small,
P{X = i} ≈ e−λ
λi i!
In other words, if n independent trials, each of which results in a “success” with probability p, are performed, then when n is large and p small, the number of successes occurring is approximately a Poisson random variable with mean λ = np. Some examples of random variables that usually obey, to a good approximation, the Poisson probability law (that is, they usually obey Equation 5.2 for some value of λ) are:
- The number of misprints on a page (or a group of pages) of a book.
- The number of people in a community living to 100 years of age.
- The number of wrong telephone numbers that are dialed in a day.
- The number of transistors that fail on their first day of use.
- The number of customers entering a post office on a given day.
Special Random Variables
Course: BS Civil Engineering
University: University of Nueva Caceres

- Discover more from:BS Civil EngineeringUniversity of Nueva Caceres678 Documents
- More from:BS Civil EngineeringUniversity of Nueva Caceres678 Documents